Annuitätendarlehen
Als Annuitätendarlehen werden in der Wirtschaft Kredite bezeichnet, die in gleichbleibenden, regelmäßigen Raten zurückgezahlt werden. Für die Mehrzahl der an private Kreditnehmer vergebenen Darlehen werden heute Annuitätendarlehen eingesetzt, sowohl bei den klassischen Ratenkrediten als auch bei der Bau- oder Immobilienfinanzierung.
Mit unseren Finanzrechnern lassen sich Annuitätendarlehen einfach berechnen. Auch die Auswirkungen von Veränderungen auf die Gesamtkosten des Darlehens sowie dessen Laufzeit lassen sich so anschaulich darstellen.
Annuitätendarlehen: Annuitätenrechner
Annuitätendarlehen bei Ratenkrediten: Kreditrechner
Kreditvergleich: Vergleich für Ratenkredite und Baufinanzierungen
Das Annuitätendarlehen unterscheidet sich damit von anderen Darlehen, wie beispielsweise dem Tilgungsdarlehen mit fester Tilgung und im Zeitverlauf abnehmenden Zins- und Ratenzahlungen oder dem endfälligen Darlehen, bei dem zunächst nur die anfallenden Zinsen zurückgezahlt werden, während am Ende der Laufzeit der gesamte Darlehensbetrag fällig wird.
Vorteile für den privaten Kreditnehmer bestehen beim Annuitätendarlehen in den konstanten Ratenzahlungen und der damit einhergehenden gleichbleibenden finanziellen Belastung: Der Kreditnehmer zahlt den Kredit in vorab festgelegten (meist monatlichen) Raten zurück und kann sich beim Ratenkredit mit festen Zinsen sowie bei der Immobilienfinanzierung während der Zinsbindung auf die Höhe der Rückzahlungen einstellen und verlassen.
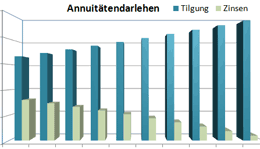
Zins und Tilgung im Zeitverlauf
Die konstanten Rückzahlungsrate (Annuität) wird beim Annuitätendarlehen dadurch erreicht, dass der Zinsanteil an den Zahlungen im Laufe der Zeit durch die geringer werdende Restschuld sinkt, während der Tilgungsanteil immer weiter steigt (siehe Grafik links). Es wird also mit zunehmender Laufzeit ein immer größerer Anteil des Darlehens zurückgezahlt, wodurch gleichzeitig die Zinsbelastung weiter sinkt. Der Kreditnehmer zahlt den Kredit dabei jedoch in konstanten Raten zurück, lediglich die letzte Zahlung kann von der festgelegten Annuität abweichen.
Annuität bei Ratenkredit und Immobilienfinanzierung
 Beim Ratenkredit ergibt sich die Annuität, d.h. die regelmäßige monatliche Ratenzahlung aus der Kreditsumme, dem Zinssatz des Darlehens sowie der Laufzeit. Kürzere Laufzeiten führen
dabei zu einer höheren monatlichen Belastung, gleichzeitig verringert sich durch die schnellere Tilgung aber auch die Summe der insgesamt durch den Kreditnehmer zu zahlenden Zinsen.
Für den Kreditnehmer gilt es daher, einen Kompromiss zwischen monatlicher Belastung und möglichst schneller Rückzahlung des Darlehens zu finden.
Beim Ratenkredit ergibt sich die Annuität, d.h. die regelmäßige monatliche Ratenzahlung aus der Kreditsumme, dem Zinssatz des Darlehens sowie der Laufzeit. Kürzere Laufzeiten führen
dabei zu einer höheren monatlichen Belastung, gleichzeitig verringert sich durch die schnellere Tilgung aber auch die Summe der insgesamt durch den Kreditnehmer zu zahlenden Zinsen.
Für den Kreditnehmer gilt es daher, einen Kompromiss zwischen monatlicher Belastung und möglichst schneller Rückzahlung des Darlehens zu finden.
Bei einer Immobilienfinanzierung wird üblicherweise nicht mit festen Laufzeiten gerechnet: Es wird wird vielmehr der Zeitraum für die Zinsbindung festgelegt, für den die Bank dem Kreditnehmer den vereinbarten Zins garantiert. Gleichzeitig wird die sogenannte "anfängliche Tilgung" vereinbart, die den Prozentsatz des Darlehens beschreibt, die der Kreditnehmer im ersten Jahr zurückzahlt. Wie beim Annuitätendarlehen üblich, steigt der Tilgungsanteil in den darauf folgenden Jahren bei sinkendem Zinsanteil und gleichbleibenden monatlichen Raten.
Auch bei der Immobilienfinanzierung stellt die Annuität einen Kompromiss aus möglichst hoher anfänglicher Tilgung (d.h. möglichst schneller Rückzahlung) und monatlicher Belastung durch die Ratenzahlungen für den Kreditnehmer dar. Durch die langen Laufzeiten können bereits geringe Unterschiede im Zinssatz sowie bei der anfänglichen Tilgung die insgesamt zu zahlenden Zinsen sowie den Zeitpunkt der vollständigen Rückzahlung des Darlehens deutlich beeinflussen.
Annuitätendarlehen: Berechnung
Die Annuität eines Darlehens bei gegebener Kreditsumme, Laufzeit und Zinssatz lässt sich unter der Annahme der vollständigen Tilgung zum Laufzeitende mit folgender Formel berechnen:
Jährliche Annuität = C0 * ANFn,i
C0 steht hierbei für die Darlehenssumme, ANFn,i für den Annuitäten- oder Wiedergewinnungsfaktor (siehe hierzu ausführlich: Kredit: Monatsrate berechnen).
Bei der Immobilienfinanzierung mit anfänglicher Tilgung ergibt sich die Annuität relativ einfach aus dem jährlichen Zins- und Tilgungsanteil:
Jährliche Annuität = C0 * (i + (Anfängliche Tilgung / 100))
Im folgenden ein Beispiel aus unserem Kreditrechner zur Veranschaulichung der Entwicklung des Zins- und Tilgungsanteils einer Annuität:
| Darlehen: 10.000€ - Zins: 5% p.a. nom. - Rate: 856,07€ - Laufzeit: 12 Monate | |||
|---|---|---|---|
| Monat: | Zinsen: | Tilgung: | Restschuld: |
| 0 | 0,00 | 0,00 | -10.000,00 |
| 1 | 41,67 | 814,41 | -9.185,59 |
| 2 | 38,27 | 817,80 | -8.367,79 |
| 3 | 34,87 | 821,21 | -7.546,58 |
| 4 | 31,44 | 824,63 | -6.721,95 |
| 5 | 28,01 | 828,07 | -5.893,88 |
| 6 | 24,56 | 831,52 | -5.062,37 |
| 7 | 21,09 | 834,98 | -4.227,39 |
| 8 | 17,61 | 838,46 | -3.388,92 |
| 9 | 14,12 | 841,95 | -2.546,97 |
| 10 | 10,61 | 845,46 | -1.701,51 |
| 11 | 7,09 | 848,99 | -852,52 |
| 12 | 3,55 | 852,52 | 0,00 |
| Gesamt: | 272,90 | 10.000,00 | 0,00 |
